Während bei expliziten Sperrklauseln (etwa der Fünf-Prozent-Hürde) genau definiert ist, wann eine Partei in ein Parlament einziehen darf und wann nicht, existiert auch bei Fehlen einer solchen expliziten Klausel eine, durch das verwendete Berechnungsverfahren gegebene Hürde zum Erlangen des ersten Sitzes.
Diese faktische Sperrklausel (oder natürliches Quorum, natürliche Sperrwirkung) muss unterschieden werden von den durchschnittlichen Stimmen pro Sitz, in der Regel reichen deutlich weniger Stimmen, um in ein Parlament einzuziehen.
Die faktische (oder systemimmanente) Sperrklausel ist dabei keine definierte Prozentzahl, sondern hängt vom Sitzzuteilungsverfahren, von der Anzahl der zu verteilenden Sitze, der Anzahl der beteiligen Parteien und des Stimmenanteils der anderen Parteien ab.
In aller Regel gibt es dabei eine untere und eine obere Grenze, d. h., eine Hürde unter der eine Partei nicht einzieht und eine Hürde über der eine Partei auf jeden Fall einzieht. Dazwischen kann eine Partei einziehen, muss es aber nicht.
Insbesondere dann, wenn viele Parteien antreten, sind die oberen und unteren Grenzen eher theoretischer Natur; praktisch konzentrieren sich die Grenzen bei mehr als 3 Parteien auf einen kleineren Bereich, abhängig vom verwendeten Sitzzuteilungsverfahren. Siehe hierzu eine grafische Darstellung.
Quotenverfahren mit Restausgleich nach größten Bruchteilen (Hare/Niemeyer)
Stimmenanteil (in Sitzanteilen)
n: Anzahl Parteien
m: Anzahl Mandate
untere Grenze (kann ab): 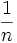
obere Grenze (muss ab):
![]() und
und
![]()
Das heißt, bei drei Parteien zieht eine Partei mit weniger Stimmen als für einen Drittel Sitz notwendig sind nicht ins Parlament ein, aber mit mehr als für zwei Drittel Sitz notwendig sind auf jeden Fall.
Bei zehn Parteien kann eine Partei ab Stimmen für 0,1 Sitze, muss aber erst ab 0,9 Sitze im Parlament vertreten sein.
Bei mehr Parteien geht die untere Hürde gegen Null und die obere Hürde gegen eins (solang auch viele Mandate zu verteilen sind), wobei allerdings eine Hürde um 0,5 Sitzanteile immer wahrscheinlicher wird.
Allgemein lässt sich sagen, dass eine Partei, die Stimmen für einen halben Sitz errungen hat, mit einer Wahrscheinlichkeit von 50 % ins Parlament einzieht (hier liegt die implizite Annahme zugrunde, dass alle Nachkommaanteile gleich wahrscheinlich sind).
Lineare Divisorverfahren (allgemeine Formel)
Formel Kopfermann S. 131 unten
Lineare Divisorverfahren sind Divisorverfahren bei denen die Stimmenzahl durch eine Folge der Form rho, rho+1, rho+2, ... dividiert wird. Dabei gilt rho=1 für d’Hondt, rho=0,5 für Sainte-Laguë bzw. rho=0 für Adams.
n: Anzahl Parteien
m: Anzahl Mandate
untere Grenze (kann ab):
![]()
obere Grenze (muß ab):
![]() und
und
![]()
Divisorverfahren mit Abrundung (d’Hondt)
untere Grenze (kann ab):
![]()
obere Grenze (muss ab) durch Hagenbach-Bischoffsche oder Droopsche Wahlzahl
![]()
Für m=30 Sitze, n=10 Parteien
kann eine Partei ab 0,7692 und muss ab 0,9677 Sitzanteil im Parlament vertreten sein.
Divisorverfahren mit Standardrundung (Sainte-Laguë)
Hier liegt die faktische Sperrklausel bei ca rho=0,5 Sitzen.
Für m=30 Sitze, n=10 Parteien
kann eine Partei ab 0,4411 und muss ab 0,5769 Sitzanteil im Parlament vertreten sein.
Modifiziertes Sainte-Laguë mit erster Divison durch 0,7
Formel siehe Kopfermann S. 133 / Lijphart-Gibberd (1977) S. 219–244
untere Grenze (kann ab)
![]()
obere Grenze (muss ab)
![]()
![]()
![]()
Für m=30 Sitze, n=10 Parteien
kann eine Partei ab 0,5865 und muss ab 0,7924 Sitzanteil im Parlament vertreten sein.
Vergleich
| Verfahren | Faktische Sperrklausel | |
|---|---|---|
| untere | obere | Für m=30 Sitze, n=10 Parteien |
| D’Hondt | 0,77 | 0,97 |
| Sainte-Laguë | 0,44 | 0,58 |
| Mod. Sainte-Laguë | 0,59 | 0,79 |
| Hare/Niemeyer | 0,10 | 0,90 |
Mythen
Es wird immer wieder geschrieben, faktische Sperrklausel sei die Stimmenzahl, die durchschnittlich zu einen Sitz führt. In Wirklichkeit reicht bspw. beim in Deutschland am häufigsten verwendeten Verfahren Hare-Niemeyer – wie oben dargestellt – im Allgemeinen aber schon die Hälfte dieser Stimmenzahl aus (und zwar nicht nur in Ausnahmefällen).
Literatur
- Klaus Kopfermann, Mathematische Aspekte der Wahlverfahren, Mannheim 1991
- Arend Lijphart, Robert William Gibberd, Thresholds and payoffs in list systems of proportional representation. European Journal of Political Research 5 (1977) 219-244.